
Plane Geometry from Envision Design (CA), is a design tool for aeromodellers. Again in this case, there is no notion of distance, but there is now a concept of smoothness of maps, for example a differentiable or smooth path (depending on the type of differential structure applied).Mike Shellim, c. From this viewpoint there are no distances, but collinearity and ratios of distances on any line are preserved.ĭifferential geometry views a plane as a 2-dimensional real manifold, a topological plane which is provided with a differential structure.

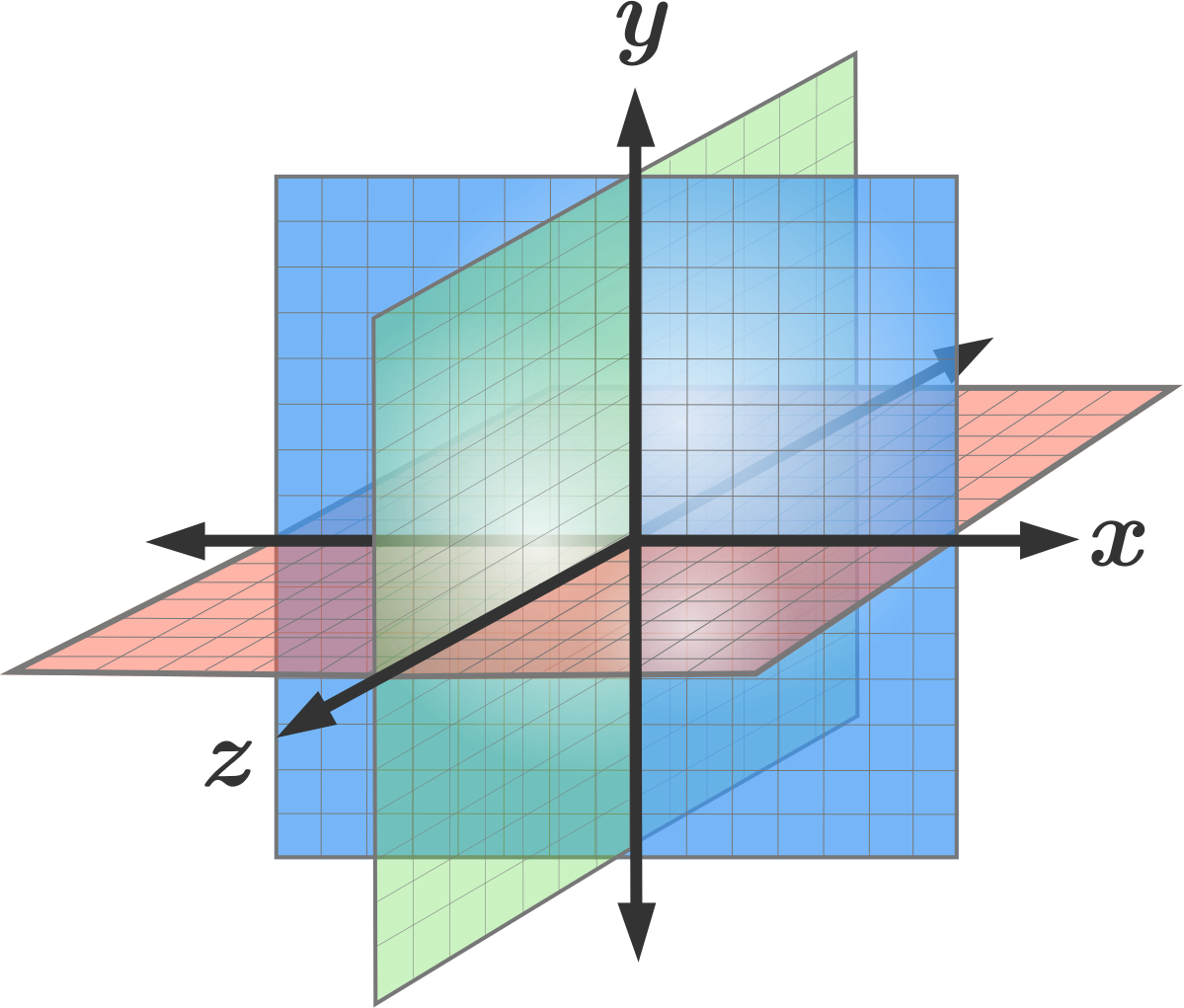
The plane may also be viewed as an affine space, whose isomorphisms are combinations of translations and non-singular linear maps. The topological plane is the natural context for the branch of graph theory that deals with planar graphs, and results such as the four color theorem. Isomorphisms of the topological plane are all continuous bijections. The topological plane, or its equivalent the open disc, is the basic topological neighborhood used to construct surfaces (or 2-manifolds) classified in low-dimensional topology. The topological plane has a concept of a linear path, but no concept of a straight line. Each level of abstraction corresponds to a specific category.Īt one extreme, all geometrical and metric concepts may be dropped to leave the topological plane, which may be thought of as an idealized homotopically trivial infinite rubber sheet, which retains a notion of proximity, but has no distances. In addition to its familiar geometric structure, with isomorphisms that are isometries with respect to the usual inner product, the plane may be viewed at various other levels of abstraction. Main article: Distance from a point to a planeįor a plane Π : a x + b y + c z + d = 0 Planes in various areas of mathematics Recalling that two vectors are perpendicular if and only if their dot product is zero, it follows that the desired plane can be described as the set of all points r such that The plane determined by the point P 0 and the vector n consists of those points P, with position vector r, such that the vector drawn from P 0 to P is perpendicular to n. Specifically, let r 0 be the position vector of some point P 0 = ( x 0, y 0, z 0), and let n = ( a, b, c) be a nonzero vector. In a manner analogous to the way lines in a two-dimensional space are described using a point-slope form for their equations, planes in a three dimensional space have a natural description using a point in the plane and a vector orthogonal to it (the normal vector) to indicate its "inclination". Point–normal form and general form of the equation of a plane Two distinct planes perpendicular to the same line must be parallel to each other.

Two distinct lines perpendicular to the same plane must be parallel to each other.A line is either parallel to a plane, intersects it at a single point, or is contained in the plane.Two distinct planes are either parallel or they intersect in a line.The following statements hold in three-dimensional Euclidean space but not in higher dimensions, though they have higher-dimensional analogues: Three non- collinear points (points not on a single line).In a Euclidean space of any number of dimensions, a plane is uniquely determined by any of the following: This section is solely concerned with planes embedded in three dimensions: specifically, in R 3.ĭetermination by contained points and lines


 0 kommentar(er)
0 kommentar(er)
